Лекции по схемотехнике, стр. 2

В общем виде логическая формула функции двух переменных записывается в виде: y=f(X₁, X₂), где X₁, X₂ — входные переменные.

В таблице истинности отображаются  все возможные сочетания (комбинации) входных переменных и соответствующие им значения функции y, получающиеся в результате выполнения какой-либо логической операции. При одной переменной полный набор состоит из четырёх функций, которые приведены в таблице 2. 

Таблица 2 – Полный набор функций одной переменной

X	Y1	Y2	Y3	Y4
0	1	0	1	0
1	0	1	1	0

Y1 — Инверсия, Y2 — Тождественная функция, Y3 — Абсолютно истинная функция и Y4 – Абсолютно ложная функция.

Инверсия (отрицание) является одной из основных логических функций, используемых в устройствах цифровой обработки информации. 

При двух переменных полный набор состоит из 16 функций, однако в цифровых устройствах используются далеко не все.

Основными логическими функциями двух переменных, используемыми в устройствах цифровой обработки информации являются: дизъюнкция (логическое сложение), конъюнкция (логическое умножение), сумма по модулю 2 (неравнозначность), стрелка Пирса и штрих Шеффера. Условные обозначения логических операций, реализующих указанные выше логические функции одной и двух переменных, приведены в таблице 3.

Таблица 3 Названия и обозначения логических операций

Операцию инверсии можно выполнить чисто арифметически: 

  и алгебраически:   Из этих выражений следует, что инверсия x, т.е.  дополняет x до 1. Отсюда и возникло ещё одно название этой операции — дополнение. Отсюда же можно сделать вывод, что двойная инверсия приводит к исходному аргументу, т.е.   и это называется законом двойного отрицания.

Таблица 4 – Таблицы истинности основных функций двух переменных

Дизъюнкция			Конъюнкция			Исключающее ИЛИ			Стрелка Пирса			Штрих Шеффера
X1	X2	Y	X1	X2	Y	X1	X2	Y	X1	X2	Y	X1	X2	Y
0	0	0	0	0	0	0	0	0	0	0	1	0	0	1
0	1	1	0	1	0	0	1	1	0	1	0	0	1	1
1	0	1	1	0	0	1	0	1	1	0	0	1	0	1
1	1	1	1	1	1	1	1	0	1	1	0	1	1	0

Дизъюнкция. В отличие от обычного арифметического или алгебраического суммирования здесь наличие двух единиц даёт в результате единицу. Поэтому при обозначении логического суммирования предпочтение следует отдать знаку (∨) вместо знака (+) [1].

Первые две строчки таблицы истинности операции дизъюнкции (x₁=0) определяют закон сложения с нулём: x ∨ 0 = x, а вторые две строчки (x₁ = 1) — закон сложения с единицей: x ∨ 1 = 1.

Конъюнкция. Таблица 4 убедительно показывает тождественность операций обычного и логическог  умножений. Поэтому в качестве знака логического умножения возможно использование привычного знака обычного умножения в виде точки [1].

Первые две строчки таблицы истинности операции конъюнкции определяют закон умножения на ноль: x·0 = 0, а вторые две — закон умножения на единицу: x·1 = x.

Исключающее ИЛИ. Под функцией «Исключающее ИЛИ» понимают следующее: единица на выходе появляется тогда, когда только на одном входе присутствует единица. Если единиц на входах две или больше, или если на всех входах нули, то на выходе будет нуль.

Надпись на обозначении элемента ИСКЛЮЧАЮЩЕЕ ИЛИ «=1» (Рисунок 1, г) как раз и обозначает, что выделяется ситуация, когда на входах одна и только одна единица.

Эта операция аналогична операции арифметического суммирования, но, как и другие логические операции, без образования переноса. Поэтому она имеет другое название сумма по модулю 2 и обозначение ⊕, сходное с обозначением арифметического суммирования.

Стрелка Пирса и  штрих Шеффера. Эти операции являются инверсиями операций дизъюнкции и конъюнкции и специального обозначения не имеют.

Рассмотренные логические функции являются простыми или элементарными, так как значение их истинности не зависит от истинности других каких либо функций, а зависит только от независимых переменных, называемых аргументами.

В цифровых вычислительных устройствах используются сложные логические функции, которые разрабатываются на основе элементарных функций. 

Сложной  является логическая функция, значение истинности которой зависит от истинности других функций. Эти функции являются аргументами данной сложной функции.

Например, в сложной логической функции

  аргументами являются X₁∨X₂ и .

1.2.2 Логические элементы 

Для реализации логических функций в устройствах цифровой обработки информации используются логические элементы. Условные графические обозначения (УГО) логических элементов, реализующих рассмотренные выше функции, приведены на рисунке 1.

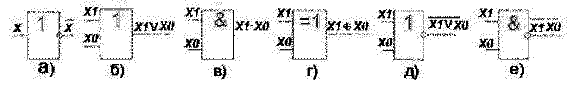
Рисунок 1 – УГО логических элементов: а) Инвертор, б) ИЛИ, в) И, г) Исключающее ИЛИ, д) ИЛИ-НЕ, е) И-НЕ.

Сложные логические функции реализуются на основе простых логических элементов, путём их соответствующего соединения для реализации конкретной аналитической функции. Функциональная схема логического устройства, реализующего сложную функцию,

, приведённую в предыдущем параграфе, приведена на рисунке 2.

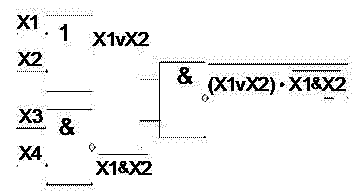
Рисунок 2 – Пример реализации сложной логической функции

Как видно из рисунка 2, логическое уравнение показывает, из каких ЛЭ и какими соединениями можно создать заданное логическое устройство.

Поскольку логическое уравнение и функциональная схема имеют однозначное соответствие, то целесообразно упростить логическую функцию, используя законы алгебры логики и, следовательно, сократить количество или изменить номенклатуру ЛЭ при её реализации.

1.2.3 Законы и тождества алгебры логики 

Математический аппарат алгебры логики позволяет преобразовать логическое выражение, заменив его равносильным с целью упрощения, сокращения числа элементов или замены элементной базы.