Теория струн и скрытые измерения вселенной, стр. 75

В результате десятимерное пространство-время получается не прямым, а, скорее, кривым произведением, часто называемым в русскоязычной литературе искривленным произведением, означающим, что эти два подпространства взаимодействуют.

Короче говоря, на расстояния в четырехмерном пространстве-времени, которые постоянно увеличиваются или искривляются, влияет шестимерная часть. Степень расширения или сжатия четырехмерного пространства-времени зависит от коэффициента искажения, и в некоторых моделях искажение представляет собой экспоненциальную функцию.

Обратимся к нашему примеру с цилиндром. Давайте представим шестимерное пространство при помощи круга. Четырехмерная часть представляет собой линию, перпендикулярную к этому кругу и мы изобразим ее отрезком линии, а не бесконечной линией, чтобы показать, как шестимерное пространство влияет на расстояния. Если искажение отсутствует, то, по мере того как вы перемещаете отрезок линии, проходя все точки круга, вы будете вычерчивать правильный сплошной цилиндр.

Однако из-за искажения длина отрезка может варьировать в процессе путешествия по кругу. В одной точке она может быть равна 1, в другой 1/2, еще в другой 1 1/2 и т. д. В результате вы получите неровный, волнистый цилиндр, который деформирован искажением. В 1986 году физик Эндрю Строминджер выразил все это через набор уравнений.

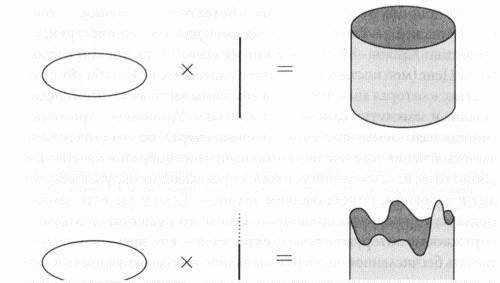
Рис. 10.7. Так называемое декартово произведение круга и отрезка линии аналогично присоединению этого же линейного сегмента к каждой единичной точке на круге. В результате получаем цилиндр. Искривленное произведение выглядит по-другому. В этом случае длина линейного сегмента не должна быть постоянным числом; она может варьировать в зависимости от ее положения на круге. Таким образом, в этом случае мы получаем не настоящий цилиндр, а объект, который можно назвать волнистым, иррегулярным цилиндром

Строминджер отмечает, что в более ранней статье 1985 года, написанной им вместе с Канделасом, Горовицом и Виттеном, где представлена первая серьезная попытка компактификации Калаби-Яу, они сделали упрощающее допущение о том, что четырехмерная и шестимерная геометрии являются независимыми. «И мы нашли решения, в которых они являются независимыми, хотя теория струн не требует этого. Годом позже я решил уравнения, которые получаются без этих допущений». Это так называемые уравнения Строминджера, которые касаются ситуации, где включаются потоки, а четырех- и шестимерные пространства взаимодействуют. «Возможность независимого существования обеих геометрий вызывает интерес, потому что из этого положения вытекает несколько действительно важных следствий», — добавляет Строминджер. Самое выдающееся из этих следствий заключается в том, что искажение может объяснить проблему иерархии масс, то есть почему масса бозона Хиггса настолько меньше планковской массы и почему гравитация настолько слабее других сил.

Уравнения Строминджера, которые применяют к не-кэлеровым многообразиям, описывают более широкий класс решений, чем уравнения, приведенные в статье 1985 года, которые применимы только к многообразиям Калаби-Яу. «Чтобы понять способы реализации теории струн в природе, необходимо понять более общие решения, — говорит Строминджер. — Важно понять все решения для теории струн, а пространство Калаби-Яу не содержит их все».[200] Гарвардский физик Ли-Шенг Ценг (мой постдок) сравнивает многообразия Калаби-Яу с окружностью, «которая является самым красивым частным случаем среди всех гладких и замкнутых одномерных кривых». Уравнения Строминджера (иногда называемые системой Строминджера), по его словам, «включают смягчение условия, определяющего многообразия Калаби-Яу, подобно тому, как смягчение условий, определяющих окружность, приводит к условиям, определяющим эллипс». Если у вас есть замкнутая петля из струны фиксированной длины, то существует только одна окружность, которую можно сделать из нее, в то время как вы можете сделать бесчисленное число разных эллипсов, взяв окружность и сжимая или раздвигая ее в разной степени. Из всех кривых, которые вы можете сделать из этой петли, окружность является единственной, которая остается инвариантной к поворотам вокруг центра.

Для того чтобы убедиться, что окружность является частным случаем эллипса, нам необходимо посмотреть на уравнение, которое определяет эллипс в декартовой системе координат (x, y): x²/a²+y²/b²=1, где a и b — положительные, действительные числа.

Кривая будет являться окружностью только при условии, что a=b. Кроме того, необходимы два параметра а и b, чтобы определить эллипс, и только один параметр (так как а=b), чтобы определить окружность. Это условие делает эллипс несколько более сложной фигурой, чем окружность, как и система Строминджера (не-кэлерова) является более сложной, чем многообразия Калаби-Яу, которые можно описать меньшим числом параметров.

Хотя переход от окружности к эллипсу и от многообразия Калаби-Яу к не-кэлерову многообразию можно считать шагом назад с точки зрения симметрии и красоты, Ценг отмечает: «очевидно, что природа не всегда выбирает самую симметричную конфигурацию. Например, подумайте об эллиптических орбитах планет. Поэтому вполне возможно, что внутренняя шестимерная геометрия, описывающая нашу естественную Вселенную, может быть не полностью симметричной, как Калаби-Яу, а чуть менее симметричной, как система Строминджера».[201]

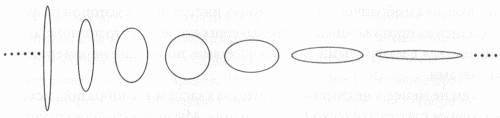
Рис. 10.8. Если у вас есть петля фиксированной длины, то вы можете сделать бесконечное число эллипсов, одни более вытянутые, другие — более округлые, но вы можете сделать только одну окружность заданной длины. Другими словами, ослабив свойства, которые определяют окружность, вы можете получить любое число эллипсов. Аналогично многообразие Калаби-Яу, которое имеет кэлерову симметрию, по определению является (как и окружность) более частным случаем, чем не-кэлерово многообразие, которое удовлетворяет менее жестким условиям и охватывает более широкий класс объектов

Система, предложенная Строминджером, отнюдь не сахар, поскольку она состоит из четырех дифференциальных уравнений, которые должны быть решены одновременно, причем каждое из них может быть кошмаром для решения. Эта система состоит из двух эрмитовых уравнений Янга-Миллса, которые предназначены для калибровочных полей (см. девятую главу). Еще одно уравнение гарантирует, что вся геометрия является суперсимметричной, а последнее предназначено для устранения аномалий, что существенно для обеспечения согласованности теории струн.

Как будто и без того задача не оказывается достаточно сложной, так вдобавок каждое из четырех уравнений фактически представляет собой систему уравнений, а не одно уравнение. Каждое из них можно записать как тензорное уравнение, но так как сам тензор содержит много переменных, то можно разделить одно уравнение на отдельные уравнения для компонентов.

По этой же причине известное уравнение Эйнштейна, которое содержит в себе всю общую теорию относительности, фактически представляет собой набор из десяти уравнений поля, описывающих гравитацию как кривизну пространства-времени, вызванную наличием вещества и энергии, несмотря на то что его можно записать как одно тензорное уравнение. При доказательстве гипотезы Калаби решение уравнений Эйнштейна в вакууме сводится к одному уравнению, хотя и довольно впечатляющему. С не-кэлеровыми многообразиями работать тяжелее, чем с многообразиями Калаби-Яу, потому что здесь наблюдается меньшая симметрия и, следовательно, больше переменных, каждая из которых ведет к увеличению числа уравнений, подлежащих решению. Кроме того, на данный момент у нас фактически нет математических инструментов для решения этой проблемы. В случае с Калаби-Яу, мы привлекли алгебраическую геометрию, инструменты которой разрабатывались на протяжении двух предыдущих столетий, что позволило нам справиться с кэлеровыми многообразиями, но не с их не-кэлеровыми коллегами.