Алекс в стране чисел. Необычайное путешествие в волшебный мир математики, стр. 37

Случайные числа нужны в промышленности и торговле. Пусть, например, некой компании, занимающейся исследованием рынка, требуется сделать опрос среди представительной выборки тысячи людей из населения в миллион. Компания использует генератор случайных чисел, чтобы создать группу выборки. Чем лучше этот генератор производит случайные числа, тем более представительной будет выборка — и тем более точным будет опрос. Подобным же образом последовательности случайных чисел требуются для симуляции непредсказуемых сценариев при тестировании компьютерных моделей. Чем более случайны числа, тем более надежны результаты теста. На самом деле возможны серьезные ошибки, если применяемые для проверки случайные числа недостаточно случайны.

— Ты хорош лишь настолько, насколько хороши твои случайные числа, — замечает Дэвид.

— Ты используешь жуткие случайные числа, но в конце концов все равно оказываешься в жуткой ситуации, — заключает Грегори.

Среди всех множеств доступных случайных чисел десятичное разложение числа ? — наилучшее.

Здесь, однако, таится некий философский парадокс. Пи, со всей самоочевидностью, не случайно. Его цифры могут вести себя как будто они случайны, но на самом деле они предопределены. Например, если бы цифры в числе ? были случайны, то шанс, что первая цифра после десятичной запятой будет равна 1, был бы равен всего 10 процентам. Однако же мы с абсолютной определенностью знаем, что там стоит 1. ? проявляет случайность не случайно — что само по себе и захватывающе, и фатально.

? — это математический концепт, который изучался тысячи лет, и тем не менее хранит в себе множество тайн. В течение почти полутора столетий, прошедших после доказательства его трансцендентности, большого прогресса в понимании природы ? не наблюдалось.

— По сути дела большая часть того, что там творится, нам неизвестна, — говорит Грегори.

Я спросил, можно ли ожидать какого-либо прогресса в отношении нашего понимания того, что же такое число ?.

— А то как же! — восклицает Грегори. — Прогресс неостановим. Математика движется вперед.

— Это будет что-то совершенно фантастическое, но это будет здорово, — подытоживает Дэвид.

Глава 5

x-фактор

Математики питают определенную склонность к волшебным фокусам. Подобные фокусы бывают забавными, а нередко скрывают за собой интересную теорию. Вот классический фокус, одновременно представляющий собой отличный способ оценить силу и достоинства алгебры. Начнем с того, что выберем любое трехзначное число, в котором первая и последняя цифры отличаются по крайней мере на два — например, 753. Теперь запишем эти же цифры в противоположном порядке: получим 357. Вычтем меньшее число из большего: 753 - 357 = 396. И наконец, сложим полученное число с тем, что получается из него перестановкой цифр в обратном порядке: 396 + 693. Сумма, которая при этом получается, равна 1089.

Попробуем еще: раз с другим числом, например 421:

Мы получили тот же самый ответ. На самом деле не имеет значения, с какого трехзначного числа мы начинаем — в конце концов всегда получится 1089. Как по волшебству, из ниоткуда возникает число 1089, подобно скале в зыбучих песках случайно выбранных чисел. Хотя устойчивое появление одного и того же результата для любого исходного числа при применении к нему всего лишь нескольких простых операций и может показаться несколько озадачивающим, тому имеется объяснение, и мы очень скоро до него доберемся. Тайна возникающего вновь и вновь числа 1089 раскрывается практически немедленно после того, как задача переписывается, но не с помощью цифр, а с помощью букв.

Хотя использование чисел просто для развлечения всегда сопутствовало математическим изысканиям, начало развития собственно математики было обусловлено необходимостью решения задач практического характера. Папирус Ринда, относящийся примерно к 1600 году до н. э. (хранится в Британском музее, а назван в честь владельца — английского египтолога А. Г. Ринда), представляет собой наиболее полный из дошедших до нас математических документов Древнего Египта. В нем содержатся 84 задачи из таких областей, как землемерие, бухгалтерский учет и разделение определенного числа хлебов на заданное число людей.

Египтяне формулировали свои задачи весьма изысканно. К примеру, задача № 30 из папируса Ринда звучит так: «Когда писец спрашивает вас, чему равна куча, если известно, что ²/₃ + ¹/₁₀ от нее составит десять, пусть он услышил правильный ответ». Здесь «куча» — египетский термин для неизвестной величины, которую в наши дни обозначают буквой x, представляющей собой фундаментальный и неотъемлемый символ современной алгебры. Сейчас бы мы задали Задачу № 30 так: чему равно значение x, если ²/₃ + ¹/₁₀ при умножении на x дает 10? Или еще короче:

Поскольку у египтян не было привычных нам математических обозначений, таких как скобки, знак равенства или иксы, они искали ответ на заданный выше вопрос методом проб и ошибок, делая оценки для «кучи». Такой метод называется правилом ложного положения, он весьма похож на игру в гольф. Когда вы уже вышли на поле, становится легче понять, как же отправить мяч в лунку. Аналогичным образом, коль скоро у вас есть какой-то ответ, пусть и неправильный, вы можете сообразить, как приблизиться к правильному. Современный метод решения, наоборот, состоит в том, чтобы сложить дроби, стоящие при переменной x, при этом уравнение

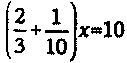
можно записать в виде

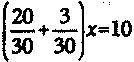
или же

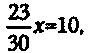
что далее сводится к

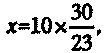
откуда, наконец,

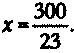
Обозначения, использующие буквы, делают жизнь куда проще.

Египетский иероглиф для сложения представлял собой пару ног, шагающих справа налево: 

(«складывающие» ноги шагают в ту сторону, в которую читается текст). Вычитание представлялось парой ног, шагающих слева направо: . По мере того как обозначения для чисел эволюционировали от палочки с насечками до современных обозначений числительных, менялись и символы арифметических операций.

У египтян, однако, не было символа для неизвестной величины; не было его и у Пифагора с Евклидом. Для них математика была по природе геометрической, связанной с тем, что можно построить. А неизвестная величина требовала следующего уровня абстракции. Диофант, живший в Александрии в III веке, первым из греческих математиков стал использовать символ для неизвестной величины. Для этой цели он выбрал греческую букву сигма — ?. Для обозначения квадрата неизвестного числа он писал ?^?, а для куба — K^?. Хотя его обозначения и были крупным достижением для того времени, поскольку позволяли сформулировать задачу более четко, они все же оставались довольно путаными, потому что — в отличие от системы, использующей x, х² и х³, — не было очевидной визуальной связи между величиной ? и ее степенями ?^? и K^?. Впрочем, несмотря на недостатки своих обозначений, Диофант вошел в историю математики как отец алгебры.