Занимательная математика, стр. 15

— У меня есть еще одна задача, которая, возможно, заинтересует вас, джентльмены, — произнес он.

— Выкладывай свою задачку, тебе слово, — предложили члены клуба. На этот раз они явно поверили в способности юного Николаса.

— Предположим, что в каждую из четырех стен этой комнаты вбито по одному гвоздю и что, кроме того, по одному гвоздю вбито в ее пол и потолок. Между этими гвоздями требуется натянуть нити. От каждого гвоздя ко всем другим должно быть протянуто по нити. Нити имеются двух цветов — красные и синие. Каждая нить, натянутая между любыми двумя гвоздями, либо красная, либо синяя.

Нити образуют много треугольников, т. е. любые три гвоздя можно рассматривать как вершины некоторого треугольника, а нити, натянутые между этими тремя гвоздями, — как стороны треугольника. Задача заключается в том, чтобы выяснить, можно ли выбрать цвета нитей так, чтобы ни у одного треугольника все три стороны не были одного цвета.

— Очень трудная задача, — задумчиво произнес математик. — Необходимо произвести комбинаторные расчеты, вычислить перестановки, сочетания и т. п. Не думаю, чтобы ты основательно разбирался во всей этой алгебре, Ник.

— А я и не разбираюсь, сэр, — почтительно ответил юный Ник, — но тем не менее могу решить эту задачу.

— Может быть, — согласился математик. — Тогда расскажи нам, как она решается.

— На самом деле задача решается очень просто, — ответил юный Николас. — Необходимо только знать, с чего начать.

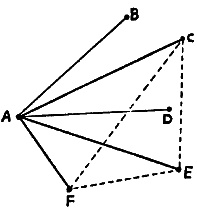
Прежде всего скажу вам ответ задачи: всегда найдется по крайней мере один треугольник, все стороны которого одного цвета. Попробую доказать, почему это так.

Рассмотрим любой гвоздь. От него к другим гвоздям должны быть протянуты пять нитей. Какие бы цвета вы ни выбрали, по крайней мере три из них должны быть одного цвета, так как нити могут быть только двух цветов — либо синие, либо красные. Для конкретности предположим, что три нити красные.

Рассмотрим теперь те три гвоздя, которые образуют вершины треугольника, между которыми протянуты эти нити.

Если мы хотим, чтобы три стороны любого треугольника не были одного цвета, то нити, натянутые между этими тремя гвоздями, не должны быть одного цвета. Попросту говоря, все стороны треугольника, к вершинам которого протянуты три красные нити, не могут быть синими. По крайней мере одна из сторон должна быть красной. Но тогда она замыкает треугольник, все стороны которого красные, а одна из вершин совпадает с исходным гвоздем.

6. Яхт-клуб

Под парусом в безветренную погоду

Однажды летом в жаркий безветренный полдень на веранде яхт- клуба собралось несколько яхтсменов. Они потягивали джин с тоником и лениво переговаривались между собой.

— Без ветра под парусом особенно не походишь, — философски заметил один из них.

— Не скажи! Иногда и в безветрие можно исхитриться, — возразил другой яхтсмен. — Как сейчас помню, однажды я прошел под парусом в полный штиль довольно приличную дистанцию.

— Штиль действительно был полным? Ни малейшего дуновения ветерка?

— Именно так!

— А как же ты управлялся с парусом?

— Как обычно.

— Может быть, ты дул себе в парус? Что ты делал?

— Ничего особенного. Я же говорю, что шел под парусом, как обычно. Чтобы было понятнее, я скажу несколько слов об обстановке. Я находился на небольшой яхте посредине реки, когда ветер внезапно упал. Ни весел, ни двигателя на яхте не было, и меня стало сносить по течению. Примерно в ста ярдах [10] прямо по курсу я увидел небольшую гребную лодку. Весла торчали по обе стороны ее корпуса, но сама лодка была пуста. Если бы мне удалось добраться до этой лодки, то я смог бы отбуксировать яхту в то место, куда направлялся. Но как преодолеть эти сто ярдов? Так как наступил полный штиль, лодку и яхту сносило вниз по течению реки с одинаковой скоростью, и расстояние между ними не сокращалось ни на дюйм [11].

— И что же ты сделал?

— Попробуй догадаться.

— Не знаю, что и думать. Вроде бы в полный штиль без весел нельзя плыть по течению быстрее, чем само течение.

— Оказывается, можно. Я сказал, что стоял полный штиль, имея в виду, что воздух был неподвижен относительно суши. Но поскольку яхту сносило вниз по течению, относительно яхты дул едва заметный бриз, направленный против течения. Ситуация была такой же, как если бы я находился на озере, а легкий ветер дул со стороны неподвижной гребной лодки. Поэтому я стал галсировать против встречного ветра и благополучно добрался до лодки.

Лодка и бутылка

— Твое решение задачи о лодке звучит прямо как специальная теория относительности Эйнштейна, — заметил один из яхтсменов.

— Речь идет всего лишь об относительном движении. В этом ты прав, но до специальной теории относительности очень далеко, — возразил другой яхтсмен, большой любитель научно-популярной литературы. — Но этот случай напомнил мне другую историю, в которой важную роль играет, какую систему координат выбрать для описания явлений.

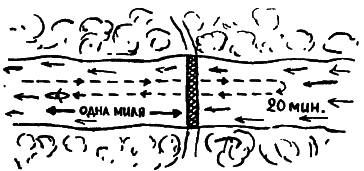
Однажды некто греб в лодке по реке против течения. На носу лодки стояла наполовину уже пустая бутылка отличного виски. Когда гребец проплывал под мостом, лодку слегка качнуло, и бутылка упала за борт. Не заметив пропажи, человек в лодке продолжал грести против течения, а бутылка между тем поплыла по течению. Через 20 минут человек заметил, что бутылка исчезла, повернул назад (временем, необходимым для совершения поворота, можно пренебречь) и поплыл вдогонку за бутылкой. Будучи от природы флегматичным, он продолжал грести в том же темпе, в каком греб против течения, но если его скорость относительно берегов до поворота была равна разности между скоростью лодки и скоростью течения, то теперь она стала равна сумме тех же скоростей. По прошествии некоторого времени гребец увидел бутылку и подобрал ее в одной миле [12] от моста (ниже его по течению).

Может ли кто-нибудь на основе этих данных сказать, какой была скорость течения?

Несколько членов клуба, любители математики, принялись решать задачу, а один из них даже составил алгебраическое уравнение, связывавшее две неизвестные величины: скорость лодки относительно воды и скорость течения реки. Но ни прямой, ни алгебраический подход не позволили решить задачу, и в конце концов знатоки пришли к заключению, что данных просто недостаточно.

— И все же решение задачи существует, причем очень простое, — заявил яхтсмен, предложивший задачу. — Необходимо лишь рассматривать задачу в системе координат, движущейся вместе с водой в реке. В такой системе координат вода в реке как бы останавливается (река превращается в озеро), а берега и мост движутся относительно системы координат. Если вы плывете на гребной лодке по озеру, уронили что-нибудь в воду и подобрали пропажу через 20 минут после того, как заметили ее, то вам понадобится ровно 20 минут, чтобы вернуться в то место, откуда вы устремились вслед за пропажей. Таким образом, бутылка пробыла в воде 40 минут, а за это время мост переместился относительно воды на 1 милю. Следовательно, скорость моста относительно воды или, что то же самое, скорость течения относительно моста и берегов составляет 1 милю за 40 минут, или 1,5 мили в час. Просто, не правда ли?

— Но вы не можете таким же способом найти скорость лодки, — заметил яхтсмен, пытавшийся решить задачу с помощью алгебраического уравнения. — Ведь в задаче две неизвестные величины.